An Overview of Image QA methods
A brief introduction of proposed methods in the literature
Peter Chng
Multimedia Coding & Communications Laboratory (MC2L)
This presentation deals with Full-Reference methods on Image Quality Assessment
Classes of methods
- PSNR/MSE
- Sub-band transforms
- Statistical
- Human Visual System (HVS)
- Structural similarity
N.B.: These are broad classes of methods and specific algorithms may use a combination of the methods described.
Classes of methods (2)
Z. Wang and A.C. Bovik's division
from Modern Image Quality Assessment- Partition based on three attributes: Knowledge of original image, distortion type and of HVS
- Reference type: Full, Reduced or Blind
- Distortion type: May be designed for evaluation specific compression schemes
- HVS may be either directly (bottom-up) or indirectly (top-down) modelled
They have adopted a more formal method, as defined below.
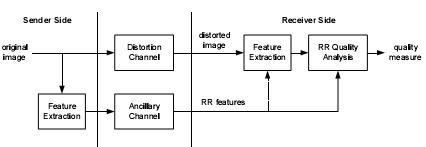
For the knowledge of the original image, full means the original, assumed perfect, image is available for comparison. Blind means only the degraded image is available for processing; most of these assume a specific distortion type. Reduced reference means that features are extracted from the original and sent to the receiver; the receiver then extracts features from the degraded image, and compares them to the original features. Most useful to track image quality when transmitted through a lossy channel.
Some methods are general, in that they do not assume any specific distortion type. Others may be designed to evaluate quality for a specific compression scheme, for example, block-DCT image compression used in JPEG, where "blockiness" is the primary type of artifact affecting quality. These methods can also be termed as "application-specific" methods. Currently blind or no-reference methods are limited to these types.
No-reference methods are especially difficult, since at least some information must be used as a guideline. For example, even when a human evaluates an image under no-reference test conditions and they look at a degraded image, internally they are comparing it to what they think they should see, based on prior knowledge and memories, which is a sort of reference.
Further explanation of what is termed "bottom-up" and "top-down" methods:
- Bottom-up
- Look at each component of the HVS, build it, and put it all together to build a functional system. Processing done at the component level.
- Top-down
- Treat the HVS as "black box", with only overall input and output are of concern. Hypothesize overall functionality of HVS (which may not be what is actually happening, but may approximate it), and design system around that. Processing done at the system level. May be much simpler.
There is no clear-cut line between these two categories, because solutions cannot ideally form the entire HVS. (As not enough is known, especially in terms of the visual cortex.) So, at least some functionality must be hypothesized; furthermore, for any system, knowledge of HVS functionality can help tweak system configuration.
PSNR/MSE
- Per-pixel based method
- Fast and easy to compute
- Does not take into account relationship between pixels
-
No idea of structure, contrast, visibility, etc.
- Images with vastly different perceived qualities may have similar MSE ratings
- Only consideration is the power of the error signal, not how it affects the image
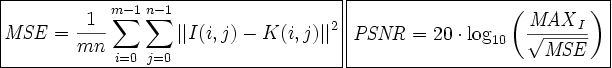
For colour images, the average MSE can be computed over the three colour bands. For PSNR, MAXI is the maximum value a pixel can obtain, usually 255.
Note that PSNR/MSE can also be computed in a different domain, for example, after a DFT is applied to the image.
PSNR/MSE (2)
- MSE is a specific form of a Minkowski metric
-
Minkowski metrics widely used to determine overall error-rates in across different sub-bands or channels
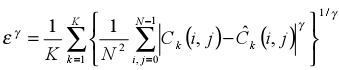
- PSNR/MSE has shown correlation > 0.9 with MOS in some image tests, so any method must be better than this to be viable
These numbers were achieved during tests on the LIVE image database, which consisted of 233 JPEG and 227 JPEG2000 images compressed at different bit rates.
Sub-band transforms
-
Decompose the image using a filter-bank and treat the "channels" differently
- Many of these techniques already used in image compression
- Channels can be treated according how it is hypothesized HVS responds to them
- Many different types used, including Block DCT, Wavelet transform, etc.
- Wavelet transforms have showed promise because they appear to correspond with HVS models
Because many of these techniques are used, many sub-band transforms in Image QA can be made to apply to only certain types of image artifacts experienced by certain compression, and their application to QA is related to the functions in image compression and processing.
Sub-band transforms (2)
Orthogonal wavelet transform
- Because wavelet filter banks operate in a cascading manner (fractal-like) decomposition resembles the cortex transform
- Additionally, wavelets (like Gabor filters) better resemble neural response
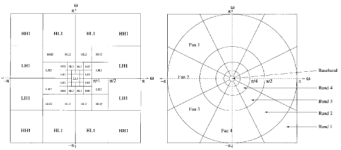
Wavelet and cortex transform decomposition in frequency domain
The basic idea behind the wavelet transform is to separate the image into high and low-pass sub-bands; the low-pass sub-band is then divided into high and low-pass sub-bands, and the process continues recursively a certain number of times, which is referred to as the level of decomposition. This is done in two dimensions for an image.
Sub-band transforms (3)
Steerable Pyramids (Simoncelli, 1995)
- Polar-separable wavelets, instead of orthogonal
- Has the advantage of no aliasing in sub-bands, resulting in translation invariance
- Thus is ideal for image quality assessment
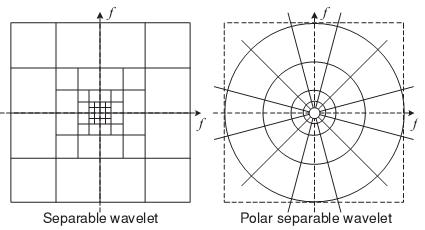
Differs from orthonormal wavelets because of the different degrees of orientations allowed for each scale or level and has the advantage of being translation-invariant and rotation-invariant. For three orientations sub-bands per level, the directions are 0, 120 and -120. However, it also is overcomplete by a factor of 4k/3, where i is the number of orientation bands.
In general, wavelet methods, (such as the Steerable Pyramids) are used in many image QA techniques. After the transform, the output can be treated differently according to the method - some look at the statistics of the coefficients, others may compare the original/test for weighted errors. Wavelet methods seem to be the most popular in image QA methods because of their resemblance to the cortex transform, and also because they're widely used in image compression.
Sub-band transforms (4)
An example decomposition using Steerable Pyramids

Decomposition using 4 orientation sub-bands at 2 different scales.
This particular example shows four orientation bands and two levels of decomposition. The orientation sub-bands represent basis functions oriented in different directions.
Statistical methods
- Treat image as signal and look at data from a statistical viewpoint
- Natural images will have certain statistical properties
- Distortion alters these statistical properties to make them unnatural
- Natural images comprise only a tiny subset of all possible images
- Statistical methods have also been used for reduced and no-reference QA for certain types of image distortions
The basic idea here is that image signals possess much structure, which in turn can be expressed statistically. Much of an image signal is redundant, so this somehow much be reflected in how the image is processed by humans. (In fact this redundancy is exploited by image compression schemes.)
Because the statistics of an image can often be evaluated independent of any reference or original signal, statistical methods have been used in reduced and no-reference techniques. Currently, no-reference methods in this area only apply to certain types of distortions, such as those experienced by JPEG compression.
Reduced-reference techniques (which will be seen soon in a later slide) will use a set of features obtained from the original for comparison. These features are usually parameters that describe the statistical distribution of coefficients from an image transform, and thus the degraded or test image's distribution can be compared to this to determine the degree-of-fit for QA purposes.
Statistical methods (2)
- Natural Scene Statistics: Sheikh, Bovik and de Veciana (2005)
-
Idea: Stimuli from natural scenes drove evolution of HVS,
thus modelling natural scenes and the HVS are dual problems
- Also: HVS less sensitive to natural distortions such as blur, white noise, brightness and contrast changes
- They chose to model natural images in the wavelet domain using GSM (Gaussian Scale Mixture) models
- Wavelet coefficients are not independent nor identically distributed (nor are they correlated), but show dependence in their variance
Natural scenes, as defined by Sheikh et al., are classified as only images in the visual environment and does not include text, computer-generated graphics, cartoons, paintings, drawings, or non-visual stimuli such as electronic displays (radar, sonar, ultrasound).
The basic process: Model a natural image's wavelet statistical properties using GSM models, then compare these statistical properties with those of the degraded or test image to get an idea of quality or the loss of fidelity.
Statistical methods (3)
From "Natural Signal Statistics and Sensory Gain Control", by O. Schwartz and E.P. Simoncelli:

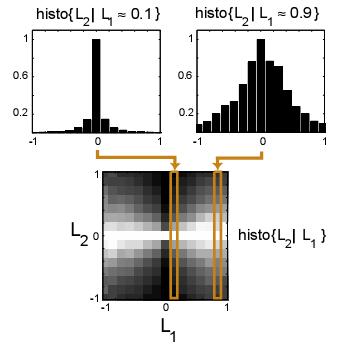
Responses of typical linear filters used in image processing to natural images often show dependency upon one another, even if filters are chosen to be orthogonal or optimized for statistical independence. The filter outputs L1 and L2 were generated by convolution of the image with the filter responses shown, which are both selective for the same spatial frequency, but have different spatial orientation and position.
The histogram of one filter response given the other shows dependence: While the mean of L2 is always zero, independent of L1, the variance of L2 depends on L1.
The case is different for nonlinear decompositions, that may well create decompositions that exhibit less statistical dependence and may be better for image encoding.
Statistical methods (4)
Distributions
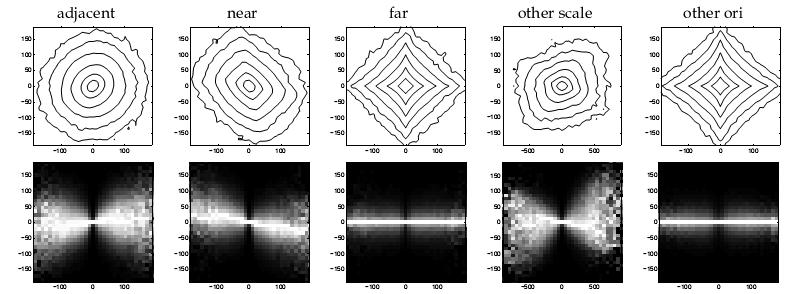
Joint distribution of wavelet coefficients and conditional distributions for varying basis functions.
Does not require any training or calibration or parameters from the HVS or viewing configuration.
Also, because the statistical properties can be expressed as parameters, statistical methods can be used in reduced-reference quality assessment.
Statistical methods (5)
Reduced-Reference Image QA (Z. Wang and E.P. Simoncelli, 2005)
- Used Steerable Pyramids to transform into wavelet domain
-
Instead of full reference image, extract a set of features and use these for comparison
- Parameters that describe statistical distribution of wavelet coefficients
- Transmitted alongside degraded image and so is ideal for monitoring image quality across a network
- Used a two-parameter generalized Gaussian density model
- Measure distortion using the Kullback-Leibler distance
An efficient model, since only two parameters are required to be sent, so not much extra bandwidth is consumed.
Statistical methods (6)

The examples show how the statistical properties of the image change when distortion is applied. (Different types of distortions produce difference changes in the histogram.) The grey dotted lines are the generalized Gaussian density model, which matches well with the original.
HVS methods
-
Model components of the HVS so that errors in different
spatial or frequency domains treated differently, as suggested by evidence of HVS
function
- This is because of retinal distribution of receptor cells
- Most HVS quality metrics depend on CSF for pre-processing the image
-
Output from CSF can be processed in different ways to determine quality
- Some methods include comparison after DCT, or sub-band/channel decomposition using wavelets
- Methods can be very complex
- In the end, errors in different channels weighted accordingly and aggregated
CSF has been empirically determined to be band-pass in nature.
HVS QA methods vary widely and may use different decompositions to separate the output from the CSF into different channels or sub-bands to weight errors differently.
While these details vary all HVS systems, by nature, use the CSF (either directly or through treating frequency sub-bands differently), to determine what image information can be obtained for quality evaluation, and by doing so hope to emulate the what goes on in the HVS.
HVS methods (2)
Contrast Sensitivity Function (CSF)
- CTF determined empirically by measuring contrast required for observer to detect sine wave gratings of varying frequencies
- CSF calculated from this
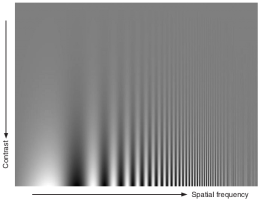
An illustration of the CSF from [1].
This illustration showing the effect of the CSF consists of sine waves along the horizontal axis and varying contrast along the vertical axis. As the frequency increases to the right, the gratings become irresolvable, no matter what the contrast, and as the contrast decreases, the same effect is observed, no matter what the frequency. The extend of the effect is of course, dependent on viewing distance, and is the result of the limit on receptor cell density on the retina.
HVS methods (3)
Masking
- An effect of the frequency-selective nature of HVS
- Result: Types of noise are less noticeable in "busy" or high-frequency parts of an image
- In particular Gaussian noise will be less visible in image areas with complex patterns
Another effect is called foveation and is the result of receptor cells concentration being the highest in the center of the retina, which is called the fovea. This results in areas of the image away from the point of focus having a lower resolution; this is why peripheral vision is not as "clear". However, it is somewhat difficult to incorporate this into the concept of Image QA since an observer may look at all parts of the image when attempting to evaluate quality. It can be however, ideal for video, where the same image is not constantly shown.
HVS methods (4)
CSF potential pitfalls
- CSF determined from tests with simple patterns (sine wave grating, etc.)
- Real-world images much more complicated; for most many simple patterns interact at the same location
-
Strength of method still mainly depends on what is used to evaluate quality after CSF
- If inter-channel interaction is not considered, error weighting may result in poor correlation with MOS
- Furthermore, HVS is a complex non-linear system while most methods attempt to model with a linear system
This may affect the performance of the CSF in relation to actual HVS perception, and these reasons are why some HVS methods fail to produce good results.
HVS methods (5)
Example HVS model: The WVDP (A.P. Bradley, 1999)
- Pre-processing to convert pixel values to luminance values to determine luminance sensitivity
- Transform both reference and test images to wavelet domain
- Normalize each by sub-band using a threshold elevation map, based on frequency (CSF)
- Determine mutual masking - are smooth areas altered significantly?
- Produce a sub-band visible error detection probability, and sum to produce the overall visible difference map
- This probability map can be used to produce a MOS
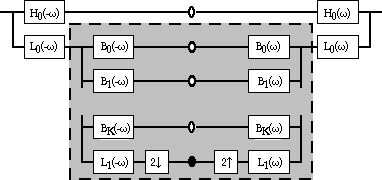
Based off of Daly's VDP, which instead used the cortex transform instead. The light-adaptation of the HVS is taken into account when determining how luminance values will be displayed on-screen, due to Weber's Law, which states that a JND depends on the overall background intensity. The CSF is not explicitly modelled, but instead takes form during the threshold elevation phase.
Many results from visual tests were used to develop this method, which still has limitations. (Probability greater than 0.5 produced for some areas of images that showed no visible differences.) This shows some of the problems typically encountered when trying to model a complex system such as the HVS.
HVS methods (6)
Example HVS model: The WVDP (A.P. Bradley, 1999)
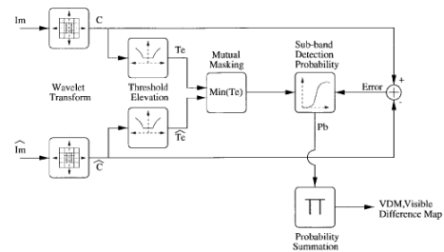
Block diagram of the WVDP
Structural similarity
Method by Wang et. al originally conceived in March 2002
- Their idea: Structural distortion related to perceived image quality
- HVS hypothetically extracts structural information during cognition
-
First quantified in their Universal Image Quality Index:
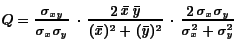
- Terms correspond to structure (correlation), luminance (mean) and contrast (variance)
- Computed separately on a sliding window, producing a quality map for the image
This method is not an HVS method per se, since it does not attempt to simulate each component of the HVS directly, but instead hypothesizes the overall functionality of the system in defining a quality metric.
Thus, it attempts to model how the HVS responds to changes in structure, contrast and luminance.
The quality map is then averaged and normalized/scaled to produce a MOS.
Structural similarity (2)
-
Universal Image Quality Index later refined to produce SSIM index
- Basically added weighting for the three terms and introduced constants to prevent near-division-by-zero
- MSSIM is their title for the averaged value of the quality indices
- Method showed promise, especially against MSE
- Somewhat surprising for such a mathematically simple metric
The changes were likely the result of empirical tests and an attempt to better correlate quality results with the MOS. The basic idea found in the Universal Image Quality Index remains unchanged.
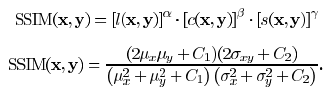
Structural similarity (3)
Problems
- Does not fare well when used on translated images (shifted, rotated)
- Did not correlate well for Gaussian-contaminated samples vs. blurred and JPEG-artifacted samples
-
Did not take into account any HVS features
- Really at the opposite end compared with methods that follow HVS step-by-step
Structural similarity (4)
Problem examples
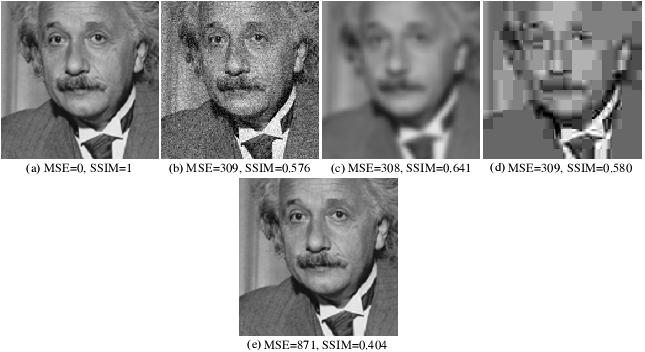
a) Original (1); b) Gaussian-contaminated (0.576); c) Blurred (0.641); d) JPEG-compressed (0.580); e) Right-shifted (0.404)
The SSIM scores do not appear to correlate with perceived quality.
The bracketed values indicate the SSIM scores. It is seen here that the Gaussian-noise contaminated image ranks close to both the blurred and JPEG-compressed image despite different quality. Personally, I would rate the Gaussian-noise contaminated image higher than both of the two. The translated image also rates significantly lower despite having practically no loss in quality.
It should be noted that most HVS Image QA methods do some sort of image alignment in a preprocessing stage to avoid translation errors.
Structural similarity (5)
- In response, Wang and Simoncelli developed the CW-SSIM index
- Used the "The Steerable Pyramids" earlier described by Simoncelli (1995)
-
This method aimed to be insensitive to image luminance/contrast and translation changes
- Transform into complex wavelet domain for comparison, since these changes lead to consistent magnitude and phase changes of local wavelet coefficients
- Thus requires no preprocessing to align images or normalize intensity
- Compare coefficients so that effect of these differences are reduced or removed
- Only works when translation/scaling/rotation is small compared with wavelet filter size
References
- Z. Wang and A.C. Bovik, Modern Image Quality Assessment, Morgan & Claypool, © 2006.
- P. Kovesi, "Phase congruency: A low-level image invariant", Psychological Research, vol. 64, pp 136-148, 2000.
- A.P. Bradley, "A Wavelet Visible Difference Predictor", IEEE Transactions on Image Processing, vol. 8, no. 5, pp 717-730, May 1999.
- K. Matkovic, "Contrast Sensitivity Function", Tone Mapping Techniques and Color Image Difference in Global Illumination.
- A. Brooks, "What makes an image look good?" The Daily Burrito, 2005.
- O. Schwartz and E.P. Simoncelli, "Natural Signal Statistics and Sensory Gain Control", Nature Neuroscience, vol. 4, no. 8, pp 819-825, August 2001.
- E.P. Simoncelli, "Statistical Modelling of Photographic Images", Handbook of Video and Image Processing, 2nd edition, section 4.7, 2005.
- E.P. Simoncelli, "The Steerable Pyramid", Laboratory for Computational Vision at NYU.
- Z. Wang et al., "Image Quality Assessment: From Error Visibility to Structural Similarity", IEEE Transactions on Image Processing, vol. 13, no. 4, pp 600-612, April 2004.
- Z. Wang and E.P. Simoncelli, "Translation Insensitive Image Similarity in Complex Wavelet Domain", ICASSP 2005, II, pp 573-576, 2005.
- Z. Want and E.P. Simoncelli, "Reduced-Reference Image Quality Assessment Using A Wavelet-Domain Natural Image Statistic Model", Human Vision and Electronic Imaging - SPIE, vol. 5666, 2005.
- H.R. Sheikh et al., "An Information Fidelity Criterion for Image Quality Assessment Using Natural Scene Statistics", IEEE Transactions on Image Processing, vol. 14, no. 12, pp 2117-2128, December 2005.
- H.R. Sheikh et al., "LIVE Quality Assessment Database", Laboratory for Image & Video Engineering.
- I. Avcibas, "Image Quality Statistics and their use in Steganalysis", Ph. D. dissertation, Institute for Graduate Studies in Science and Engineering, Bogazici University, 2001
The entire contents of this presentation are available at my website.
Thank you!
Questions/Comments?